Syllabus:-
Assignment 1:-
1 Define Algorithm. Discuss key characteristics of algorithm. Why do we need to analyse algorithms?
Algorithm is a step-by-step procedure, which defines a set of instructions to be executed in a certain order to get the desired output.
Characteristics of an Algorithm
- Not all procedures can be called an algorithm. An algorithm should have the following characteristics −
- Unambiguous − Algorithm should be clear and unambiguous. Each of its steps (or phases), and their inputs/outputs should be clear and must lead to only one meaning.
- Input − An algorithm should have 0 or more well-defined inputs.
- Output − An algorithm should have 1 or more well-defined outputs, and should match the desired output.
- Finiteness − Algorithms must terminate after a finite number of steps.
- Feasibility − Should be feasible with the available resources.
- Independent − An algorithm should have step-by-step directions, which should be independent of any programming code.
Why Analysis of Algorithms is important?
- To predict the behavior of an algorithm without implementing it on a specific computer.
- It is much more convenient to have simple measures for the efficiency of an algorithm than to implement the algorithm and test the efficiency every time a certain parameter in the underlying computer system changes.
- It is impossible to predict the exact behavior of an algorithm. There are too many influencing factors.
- The analysis is thus only an approximation; it is not perfect.
- More importantly, by analyzing different algorithms, we can compare them to determine the best one for our purpose.
2 What do you mean by asymptotic notation? Describe in brief asymptotic notations: Omega, Theta, Big O.
Asymptotic Notations are languages that allow us to analyze an algorithm's running time by identifying its behavior as the input size for the algorithm increases. This is also known as an algorithm's growth rate.
Omega Notation (Ω-notation)
Omega notation represents the lower bound of the running time of an algorithm. Thus, it provides the best case complexity of an algorithm.

Omega gives the lower bound of a function
Ω(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }
Theta Notation (Θ-notation)
Theta notation encloses the function from above and below. Since it represents the upper and the lower bound of the running time of an algorithm, it is used for analyzing the average-case complexity of an algorithm.
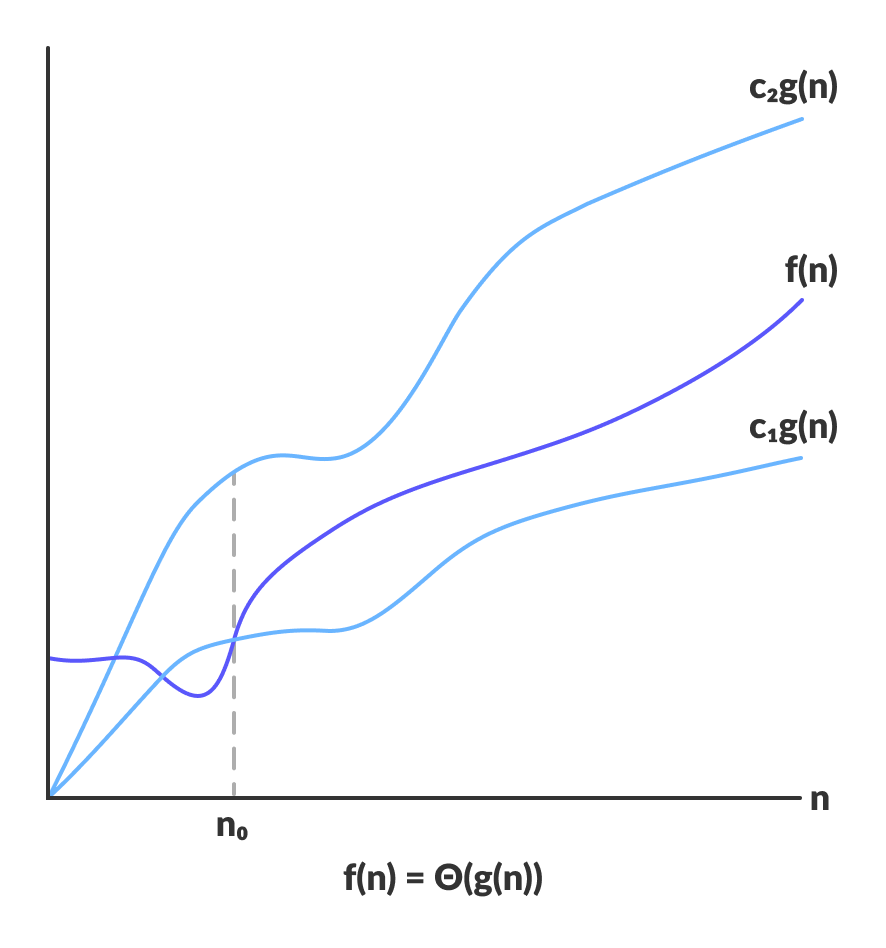
Theta bounds the function within constants factors
Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }
Big-O Notation (O-notation)
Big-O notation represents the upper bound of the running time of an algorithm. Thus, it gives the worst-case complexity of an algorithm.
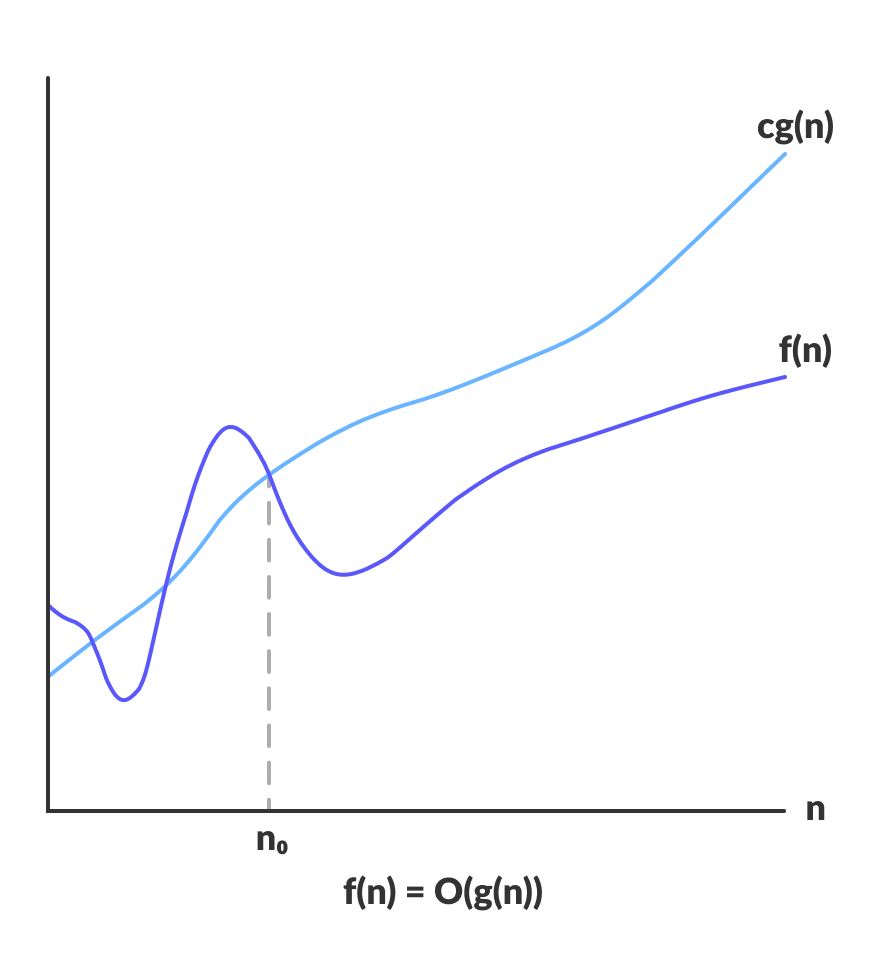
Big-O gives the upper bound of a function
O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }
3 Apply the bubble sort algorithm for sorting {U, N, I, V, E, R, S}. What is the time complexity of bubble sort?
If you Know then Email me Solution or Contact Us Page.
4 Explain an algorithm for Selection Sort Algorithm. Derive its time complexity.
ALGORITHM: SELECTION SORT (A)
1. k ← length [A]
2. for j ←1 to n-1
3. smallest ← j
4. for I ← j + 1 to k
5. if A [i] < A [ smallest]
6. then smallest ← i
7. exchange (A [j], A [smallest])
Complexity Analysis of Selection Sort
Input: Given n input elements.
Output: Number of steps incurred to sort a list.
Logic: If we are given n elements, then in the first pass, it will do n-1 comparisons; in the second pass, it will do n-2; in the third pass, it will do n-3 and so on. Thus, the total number of comparisons can be found by;
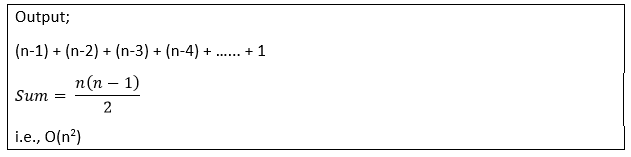
Selection Sort
Therefore, the selection sort algorithm encompasses a time complexity of O(n^2) and a space complexity of O(1) because it necessitates some extra memory space for temp variable for swapping.
5.What is the best case and worst case complexity of insertion sort? Derive them
If you Know then Email me Solution or Contact Us Page.
6. 15, 19, 10, 7, 17, 16 - sort it in ascending order using heap sort.
If you Know then Email me Solution or Contact Us Page.
7. What is a stable sort? Give example of stable and non-stable sort algorithms.
A Stable Sort is one which preserves the original order of input set, where the comparison algorithm does not distinguish between two or more items. A Stable Sort will guarantee that the original order of data having the same rank is preserved in the output.
examples of stable algorithms are Merge Sort, Insertion Sort, Bubble Sort and Binary Tree Sort. While, QuickSort, Heap Sort, and Selection sort are the unstable sorting algorithm.
8 R = {cat, him, ham, bat}. Sort R using radix sort.
If you Know then Email me Solution or Contact Us Page.
9 Name the sorting algorithms which can sort in linear amount of time.
There is some algorithm that runs faster and takes linear time such as Counting Sort, Radix Sort, and Bucket Sort.
10 Which are the basic steps of counting sort? Write counting sort algorithm. Derive its time complexity in worst case.
Steps:-
- Find out the maximum element (let it be max) from the given array
- Initialize an array of length max+1 with all elements 0. This array is used for storing the count of the elements in the array.
- Store the count of each element at their respective index in count array
- Store cumulative sum of the elements of the count array. It helps in placing the elements into the correct index of the sorted array.
- Find the index of each element of the original array in the count array. This gives the cumulative count. Place the element at the index calculated as shown in figure below
- After placing each element at its correct position, decrease its count by one
Counting Sort Algorithm
countingSort(array, size)
max <- find largest element in array
initialize count array with all zeros
for j <- 0 to size
find the total count of each unique element and
store the count at jth index in count array
for i <- 1 to max
find the cumulative sum and store it in count array itself
for j <- size down to 1
restore the elements to array
decrease count of each element restored by 1Worst Time Complexity Of Counting Sort:-
If you Know then Email me Solution or Contact Us Page.



0 Comments