Artificial Intelligence Assignments

 

Assignment 1 (Introduction and Search Techniques)

1. Explain state space representation of the Missionaries and Cannibals problem

Problem: Three missionaries and three cannibals, along with one boat that fits at most two people ( and requires at least one for operation), are on the left bank of a river. The most salient thing about missionaries and cannibals in “cohabitation” is that if ever the cannibals in any one spot (left bank, right bank, on the boat outnumber the missionaries, the outnumbered missionaries will be consumed – eaten! The goal of this problem is to get all six individuals safely across the river from the left bank to the right bank. 

Objects of the State World: 

M M M C C C B 

3 missionaries, 3 cannibals, 1 boat, a left river bank, and a right river bank. C represents a cannibal, M represents a missionary, and B represents the location of the boat. 

Representation of a State of the World: 

L R A state of the world is represented as 2 lists : L is the left bank. R is the right bank. C represents the location’s amount of cannibals. M represents the location's amount of missionaries. B is 1 when the boat is on the shore and 0 when it is on the opposite shore.

2. Consider the following initial and goal configuration for 8-puzzle problem. Draw the search tree. Apply A* algorithm to reach from initial state to goal state and show the solution. Consider Manhattan distance as a heuristic function (i.e. sum of the distance that the tiles are out of place.) 

If Anyone Knows This Question Just Mail Answer Or Write Down in Comments Section

3. Analyze N-queen problems with respect to the following problem characteristics: 

a. Is the problem decomposable? 
b. Can solution step be ignored? 
c. Is the good solution absolute or relative? 
d. Is the solution state or a path? 
e. What is the role of knowledge?

A) Can the problem be broken down into smaller problems to be solved independently?

The decomposable problem can be solved easily.

Example: In this case, the problem is divided into smaller problems. The smaller problems are solved independently. Finally, the result is merged to get the final result.

B) Yes, Such problems are called Ignorable problems.

In the 8-Puzzle, Moves can be undone and backtracked.

Such problems are called Recoverable problems.

In Playing Chess, moves can be retracted.

Such problems are called Irrecoverable problems.

Ignorable problems can be solved using a simple control structure that never backtracks. Recoverable problems can be solved using backtracking. Irrecoverable problems can be solved by recoverable style methods via planning.

C)The Travelling Salesman Problem, we have to try all paths to find the shortest one.

Any path problem can be solved using heuristics that suggest good paths to explore.

For best-path problems, a much more exhaustive search will be performed.

D) The Water Jug Problem, the path that leads to the goal must be reported.

A path-solution problem can be reformulated as a state-solution problem by describing a state as a partial path to a solution. The question is whether that is natural or not.

E) Role of Knowledge in Computing:

Playing Chess

Consider again the problem of playing chess. Suppose you had unlimited computing power available. How much knowledge would be required by a perfect program? The answer to this question is very little—just the rules for determining legal moves and some simple control mechanism that implements an appropriate search procedure.
Additional knowledge about such things as good strategy and tactics could of course help considerably to constrain the search and speed up the execution of the program. Knowledge is important only to constrain the search for a solution.

Reading Newspaper

Now consider the problem of scanning daily newspapers to decide which are supporting the Democrats and which are supporting the Republicans in some upcoming election. Again assuming unlimited computing power, how much knowledge would be required by a computer trying to solve this problem? This time the answer is a great deal.

4. What do you mean by Hill climbing strategy? Explain in brief types of Hill Climbing. Also discuss problems arise and its solution in Hill Climbing strategy.

Hill Climbing is a heuristic search used for mathematical optimization problems in the field of Artificial Intelligence. Given a large set of inputs and a good heuristic function, it tries to find a sufficiently good solution to the problem. This solution may not be the global optimal maximum.

Types of Hill Climbing Algorithm:

• Simple hill Climbing:
• Steepest-Ascent hill-climbing:
• Stochastic hill Climbing:

1. Simple Hill Climbing:

Simple hill climbing is the simplest way to implement a hill climbing algorithm. It only evaluates the neighbor node state at a time and selects the first one which optimizes current cost and set it as a current state. It only checks it's one successor state, and if it finds better than the current state, then move else be in the same state. 

2. Steepest-Ascent hill climbing:

The steepest-Ascent algorithm is a variation of simple hill climbing algorithm. This algorithm examines all the neighboring nodes of the current state and selects one neighbor node which is closest to the goal state. This algorithm consumes more time as it searches for multiple neighbors

3. Stochastic hill climbing:

Stochastic hill climbing does not examine for all its neighbor before moving. Rather, this search algorithm selects one neighbor node at random and decides whether to choose it as a current state or examine another state.

Problems in Hill Climbing Algorithm:

1. Local Maximum: A local maximum is a peak state in the landscape which is better than each of its neighboring states, but there is another state also present which is higher than the local maximum.

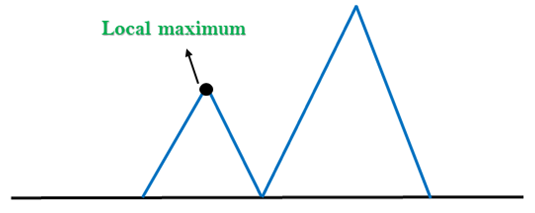
Solution: Backtracking technique can be a solution of the local maximum in state space landscape. Create a list of the promising path so that the algorithm can backtrack the search space and explore other paths as well.

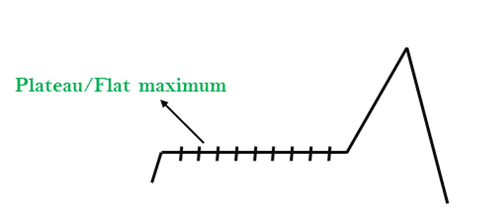
2. Plateau: A plateau is the flat area of the search space in which all the neighbor states of the current state contains the same value, because of this algorithm does not find any best direction to move. A hill-climbing search might be lost in the plateau area.

Solution: The solution for the plateau is to take big steps or very little steps while searching, to solve the problem. Randomly select a state which is far away from the current state so it is possible that the algorithm could find non-plateau region.

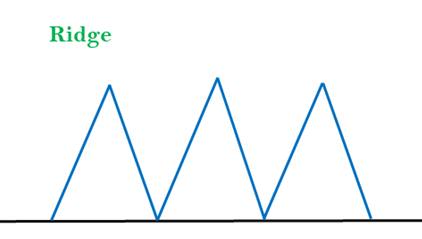
3. Ridges: A ridge is a special form of the local maximum. It has an area which is higher than its surrounding areas, but itself has a slope, and cannot be reached in a single move.

Solution: With the use of bidirectional search, or by moving in different directions, we can improve this problem.

5. Solve following Crypt arithmetic problems:

  P O I N T 
    +   Z E R O
    -----------
    E N E R G Y

Step 1

• E is 1 as max carry possible is 1
• P + (nothing) = N, it should have had been P
• This means that there is a carry from previous step
• P + 1 (carry) >10 as it gives Carry at next step to result E
• Thus, P = 9
• E = P + 1 = 0 (1 carry)

So, E = 1, P = 9, N = 0

Since, the problem contains both 0 and O we will replace O by X to avoid confusion.

    1 1
      9 O I 0 T 
    +   Z 1 R O
    -----------
    1 0 1 R G Y

Step 2

• In, column 2, R + 0 = G, this means there must be 1 carry from previous step
• Thus, G = R + 1 that means they are consecutive and G >R
• Similarly, in column 3, R = I + 1. This means I and R as consecutive, with R >G
• Since, G = R + 1 and R = I + 1 => G = (I + 1) + 1 => G = I + 2
• Thus, G, R and I are consecutive, with G > R > I.

Step 3

• T + O = Y

    1 1     1
      9 O I 0 T 
    +   Z 1 R O
    -----------
    1 0 1 R G Y

Step 3

• T + O > 10, as its generating carry on next step.
• It will also not be 10 or 11 as T + O = Y and Y cant be 0 or 1 as those values are already taken.
• So lets assume T + O to be 12. Thus, Y = 2
• Possible values can be –
• T, O = (3, 9) not possible as 9 already taken
• T, O = (4, 8) possible as unoccupied, let’s try this.

    1 1     1
      9 8 I 0 4 
    +   Z 1 R 8
    -----------
    1 0 1 R G 2

Step 4

• Till now the values are –
• N = 0, E = 1, Y = 2, T = 4, O = 8, P = 9
• Remaining values are 3, 5, 6, 7
• Now, Z + 8 = 11 
• Thus, Z has to be 3

And since, we already know G, R, I are consecutive, thus, they are 5, 6, 7

So, E + N + E + R + G + Y = 1 + 0 + 1 + 6 + 7 +2 = 17